Какой физической величиной является температура векторной или скалярной

Температура является физической скалярной величиной. Почему? Какие физические величины являются скалярными, какие – векторными? Alen4uk 2 года назад Доля начала стоит вспомнить, что же такое скалярная, а что такое векторная величина. В этом нам поможет схема. Как видим, скалярные величины имеют только числовое значение. Поэтому температура относится к скалярным величинам, имеющей только числовое значение. К скалярным величинам так же относится путь, масса, время и т.д. А вот скорость, сила, магнитная индукция относятся к векторным величинам, так как они помимо числового выражения, имеют еще и направление. Так, мы каждое утро стараемся посмотреть погоду, где нас интересует скорость, а так же направление ветра, от них зависит как нам одеваться, выходя на улицу. автор вопроса выбрал этот ответ лучшим Ужевсёсказано 2 года назад Что такое скалярная величина? Это такая величина, которую можно выразить каким-нибудь числом. А что такое векторная величина? Это величина, которая имеет какое-либо направление (в самом слове вектор заложен такой смысл). Поэтому у температуры есть конкретное число, например, 36 и 6 – идеальная темп-ра тела – это физическая скалярная величина, а вот скорость с которой она будет повышаться или понижаться будет векторной величиной, направленной в ту или иную сторону. Именно поэтому температура явл-ся физической скалярной вел-ой, а не векторной. Ниже можно посмотреть примеры и различия скаляров и векторов: Алиса в Стране 2 года назад Векторные величины, как это понятно уже из самого их названия, величины, которые имеют направление, вектор, например, скорость или сила, температура же не имеет направления, она имеет только значение – большее или меньшее, направления у нее нет, поэтому ее мы и относим к скалярным величинам. Galina7v7 более года назад Судя по определению скалярной и векторной величин, отличаются они только тем, что в векторной величине есть направление.То есть в температуре есть её величина, пусть со знаком + или минус, но это величина. И в данный определённый момент времени эта физическая величина определяется только конкретным значение: +25 ºС, или -15 ºС, запись по шкале Цельсия. В данной точке нельзя определить направление изменения температуры, она может изменяться в любом направления около указанного значения, или изменяться скачками. Хотя иногда многих сбивает то, что температуру часто изображают в виде графика изменения, и в каждой точке она или растёт , или уменьшается. Потому и определяется температура, как скалярная, что две соседние точки графика температуры относительно времени, сравниваются по их величине, но не по направлению. Скалярные величины: масса m, но не вес, путь s, температура t, векторные величина: скорость v, ускорение a, вес P,сила f, и множество аналогов из теории электричества и магнетизма. габбас 2 года назад Температура – это одна из физических величин, смысл которой трудно понять. Все знают, что более горячие тела имеют более высокую температуру и наоборот. Только после создания молекулярно-кинетической теории (Больцман, Авогадро, Менделеев, Клапейрон и другие) стало понятно, что температура характеризует энергию (является мерой средней кинетической энергии частиц). Понятно, что при таком определении температуры, становится понятным, почему температура Солнца очень высокая, почему существует низший предел (абсолютный нуль) температуры. И понятно, что температура скалярная величина, то есть она может быть только больше или меньше, меняется только по величине. А векторные величины (скорость, сила, ускорение, …) могут меняться еще и по направлению. tana76 2 года назад Физические величины делятся на две большие категории. Одни – скалярные, которые могут быть выражены лишь в виде определенного показателя – значения. Например, температура, рост, молярная масса, высота, время, плотность, энергия. Другие величины, кроме значения, имеют еще и направление действия – то есть они оцениваются сразу двумя параметрами: значением и направлением. К этой категории величин относятся сила (давления, притяжения, трения), скорость, ускорение. При определении суммы этих величин производятся действия с векторами. Знаете ответ? |
Источник
- Главная
- Вопросы & Ответы
- Вопрос 256129
Таня Масян
более месяца назад
Просмотров : 4
Ответов : 1
Лучший ответ:
Онтонио Веселко
векторное-имеет напрвлениескалярное не имеет напрвление.РЕШИ ТЕПЕРЬ ТЫ МНЕ!!!
велосипедист едет равномерно со скоростью 25 км/ч его обгоняет мотоциклист едущий со скоростью 75 км/ч.Изобразите графически скорости их движения.Выберите масштаб: 1 см-_____км
ГРАФИК-НЕОБЯЗАТЕЛЬНО,ТОЛЬКОЛ ЗАДАЧУ!!!!!!!!!
более месяца назад
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт

Лучшее из галереи за : неделю месяц все время































Другие вопросы:
Энджелл
Как сказать по-другому “потеря любви равносильна потере жизни”?
более месяца назад
Смотреть ответ
Просмотров : 12
Ответов : 1
Главный Попко
Доказательство того что моллюски стоят на более высокой стурени эволюцыонного развития чем черви
более месяца назад
Смотреть ответ
Просмотров : 7
Ответов : 1
Онтонио Веселко
Помогите пожалуйста с географией.Докажите, что и в наше время продолжается процесс формирования рельефа. Заранее спасибо.
более месяца назад
Смотреть ответ
Просмотров : 7
Ответов : 1
Зачетный Опарыш
Какой объём кислорода необходим для сжигания 4л. метана?
более месяца назад
Смотреть ответ
Просмотров : 4
Ответов : 1
Зачетный Опарыш
внутренняя энергия 1 кг меди увеличилась га 160 Дж. На сколько градусов нагрели кусок меди?
более месяца назад
Смотреть ответ
Просмотров : 10
Ответов : 1
Источник
Пугающие школьника два слова – вектор и скаляр – на самом деле не являются страшными. Если подойти к теме с интересом, то все можно понять. В данной статье рассмотрим, какая величина является векторной, а какая скалярной. Точнее, приведем примеры. Каждый ученик, наверное, обращал внимание, что в физике некоторые величины обозначаются не только символом, но и стрелкой сверху. Что они обозначают? Об этом будет сказано ниже. Постараемся разобраться, чем отличается векторная величина от скалярной.
Примеры векторов. Как они обозначаются
Что подразумевается под вектором? То, что характеризует движение. Не важно, в пространстве или на плоскости. Какая величина является векторной вообще? Например, летит самолет с определенной скоростью на какой-то высоте, имеет конкретную массу, начал движение из аэропорта с нужным ускорением. Что относится к движению самолета? Что заставило его лететь? Конечно, ускорение, скорость. Векторные величины из курса физики являются наглядными примерами. Говоря прямо, векторная величина связана с движением, перемещением.
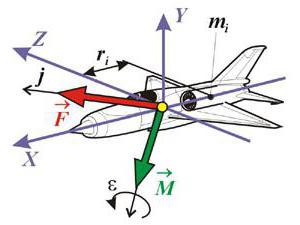
Вода тоже движется с определенной скоростью с высоты горы. Видите? Движение осуществляется за счет не объема или массы, а именно скорости. Теннисист дает возможность мячику двигаться при помощи ракетки. Он задает ускорение. К слову сказать, приложенная в данном случае сила также является векторной величиной. Потому что она получается вследствие заданных скоростей и ускорений. Сила способна также меняться, осуществлять конкретные действия. Ветер, который колышет листья на деревьях, тоже можно считать примером. Так как имеется скорость.
Положительные и отрицательные величины
Векторной величиной называется величина, которая имеет направление в окружающем пространстве и модуль. Снова появилось пугающее слово, на этот раз модуль. Представьте, что нужно решить задачку, где будет фиксироваться отрицательное значение ускорения. В природе отрицательных значений, казалось бы, не существует. Как скорость может быть отрицательной?
У вектора есть такое понятие. Это касается, например, сил, которые приложены к телу, но имеют разные направления. Вспомните третий закон Ньютона, где действие равно противодействию. Ребята перетягивают канат. Одна команда в синих футболках, вторая – в желтых. Вторые оказываются сильнее. Допустим, что вектор их силы направлен положительно. В то же время у первых не получается натянуть канат, но пытаются. Возникает противодействующая сила.
Векторная или скалярная величина?
Поговорим о том, чем отличается векторная величина от скалярной. Какой параметр не имеет никакого направления, но имеет свое значение? Перечислим некоторые скалярные величины ниже:
- время (секунда, минута, день, год);
- масса (грамм, килограмм, тонна);
- длина, расстояние (сантиметр, метр, километр);
- площадь и объем (метр квадратный и кубический);
- температура (градус Цельсия, Фаренгейт);
- доза радиации, излучения (бар, рентген);
- уровень шума, вибрации (децибел).
Имеют ли все они направление? Нет. Какая величина является векторной, а какая скалярной, можно показать только наглядными примерами. В физике есть такие понятия не только в разделе “Механика, динамика и кинематика”, а так же в параграфе “Электричество и магнетизм”. Сила Лоренца, индукция, магнитное поле – все это так же векторные величины.
Вектор и скаляр в формулах
В учебниках по физике часто встречаются формулы, в которых есть стрелочка сверху. Вспомните второй закон Ньютона. Сила (“F” со стрелочкой сверху) равна произведению массы (“m”) и ускорения (“a” со стрелочкой сверху). Как говорилось выше, сила и ускорение являются величинами векторными, а вот масса – скалярной.
К сожалению, не во всех изданиях есть обозначение этих величин. Наверное, сделано это для упрощения, чтобы школьников не вводить в заблуждение. Лучше всего покупать те книги и справочники, в которых обозначены векторы в формулах.
То, какая величина является векторной, покажет иллюстрация. Рекомендуется обращать внимание на картинки и схемы на уроках физики. Векторные величины имеют направление. Куда направлена сила тяжести? Конечно же, вниз. Значит, стрелочка будет показана в том же направлении.
В технических вузах изучают физику углубленно. В рамках многих дисциплин преподаватели рассказывают о том, какие величины являются скалярными и векторными. Такие знания требуются в сферах: строительство, транспорт, естественные науки.
Источник
«Что-то я не помню такой темы в физике» — первое, что, наверное, пришло вам в голову. Да, вы правы — тема незаметная, но в некоторых учебниках она присутствует. «А нужна она мне для ЕГЭ?» Нужна. Точно нужна. Очень нужна. Постоянно нужна.
Давайте приступим. Надо запомнить, что в физике (школьной) есть два типа физических величин:
- скалярная величина;
- векторная величина.
Скалярная величина — это просто число. Ну, например, масса тела MMM — это скалярная величина. Пусть, например, M=3M = 3M=3 кг. Время ttt — скалярная величина. Например, время может быть такое: t=7t = 7t=7 сек.
Векторная величина. Что это такое? Давайте вспомним (а для тех, кто не знал — узнаем), что
вектор — это направленный отрезок.
Стрелка — по-простому. У стрелки (вектора) есть длина (длина стрелки) и направление. Вектор — это нечто, что обладает длиной и направлением.
Примеры векторных величин: сила F⃗vec {F}F⃗, скорость V⃗vec{V}V⃗.
Длина вектора обозначается специальным символом — символом модуля | | — это две параллельные палочки. Например, ∣F⃗∣|vec{F}|∣F⃗∣ — модуль силы; ∣V⃗∣|vec{V}|∣V⃗∣ — модуль скорости. Модуль вектора — это уже число. Например, может быть так, что модуль силы ∣F⃗∣=8|vec{F}|=8∣F⃗∣=8 H, модуль скорости ∣V⃗∣=8|vec{V}|=8∣V⃗∣=8 м/с.
Направление вектора изображается на картинке. Куда показывает вектор — туда он и направлен. Например, бывает так, что вектор направлен вверх, вниз и т.д. Вектор может быть направлен вдоль какой-то плоскости. Примеры можете видеть на картинках.
Может возникнуть вопрос: а как отличить векторную величину от скалярной? Или так: как я узнаю, что передо мной вектор, а не скаляр?
Ну, самое простое — это опыт. Решая задачи, читая теоретический материал, вы со временем запомните, какие величины векторные, а какие скалярные. Физических величин не так много, как может показаться.
А способ чуть посложнее — это представить эти величины и решить для себя: могут они иметь направление? Если да — то это вектор, если нет — скаляр.
Например: заряд конденсатора. Если заряд имеет направление, то куда он направлен? Непонятно — поэтому, скорее всего, заряд — это скалярная величина.
Другой пример: длина отрезка. Если эта физическая величина имеет направление, то откуда куда она направлена: от точки 1 до точки 2? Или от точки 2 до точки 1? Трудно выбрать — поэтому, скорее всего, длина отрезка — это скаляр.
Какие из представленных на рисунках величин являются скалярными, а какие — векторными?
а) Длина отрезка
Скаляр
Вектор
б) Скорость автомобиля V⃗vec{V}V⃗
Скаляр
Вектор
в) Сила притяжения луны землей F⃗vec{F}F⃗
Скаляр
Вектор
г) Объем воздушного шара VVV
Скаляр
Вектор
д) Путь SSS из пункта А в пункт B
Скаляр
Вектор
е) Перемещение r⃗vec{r}r⃗ из пунтка А в пункт B
Скаляр
Вектор
“Ну и что?” — спросите вы. “Ну и то”, — ответим мы. Все это было введение. Самое интересное (или лучше — самое нужное) — это то, что можно делать со скалярными величинами и с векторами.
Со скалярными величинами ничего сложного — это же просто числа. Их складывают, вычитают, умножают, делят, возводят в степень, берут корень и т.д. Например, если масса одного бруска m1=2m_1 =2m1=2 кг, а масса другого бруска m2=3m_2=3m2=3 кг, то вместе они образуют тело массой m=2+3=5m=2+3=5m=2+3=5 кг.
С векторами можно делать почти все то же самое, но делается это немного странно.
Сложение векторов
1. Сложение векторов будем разбирать на конкретном примере. Пусть на шарик действуют силы F1⃗vec{F_1}F1⃗ и F2⃗vec{F_2}F2⃗. Оказывается, их можно заменить одной силой, если сложить.
Как складывать? Есть два способа:
а) Метод параллелограмма (прямоугольника);
б) Метод тругольника.
а) Метод параллелограмма (прямоугольника). Если нужно сложить два вектора a⃗vec {a}a⃗ и b⃗vec{b}b⃗, то нужно перенести параллельно вектор a⃗vec{a}a⃗ и отложить от конца вектора b⃗vec{b}b⃗. Аналогично с вектором b⃗vec{b}b⃗: переносим его параллельно и откладываем от конца вектора a⃗vec{a}a⃗. Должен получиться параллелограмм. Или прямоугольник (если повезет). Теперь соединяем начало исходных векторов a⃗vec{a}a⃗ и b⃗vec{b}b⃗ с противоположной вершиной параллелограмма. Получаем вектор c⃗=a⃗+b⃗vec{c}=vec{a}+vec{b}c⃗=a⃗+b⃗.
б) Метод треугольника. Это альтернативный способ. Хотя по сути в нем все тоже самое. Пусть опять же есть два вектора a⃗vec {a}a⃗ и b⃗vec{b}b⃗. Берем любой из них. Например, берем вектор b⃗vec{b}b⃗ и переносим его начало в конец вектора a⃗vec{a}a⃗. Получился почти треугольник. Соединяем начало вектора a⃗vec{a}a⃗ и конец вектора b⃗vec{b}b⃗ — это и есть вектор c⃗vec{c}c⃗.
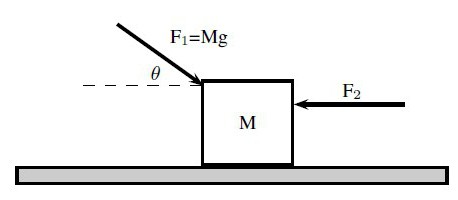
К телу приложены две силы F1F_1F1 и F2F_2F2.
Какой вектор показывает правильное направление суммарной силы (суммы векторов)?
1
2
3
4
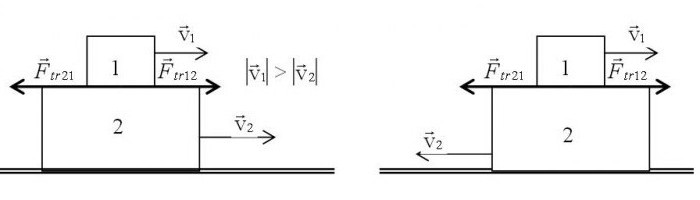
Доска двигается со скоростью V1V_1V1 относительно стола. Шарик катится по доске со скоростью V2V_2V2 относительно доски.
Какой вектор показывает правильное направление для суммарной скорости шарика относительно стола?
1
2
3
4
Умножение вектора на число
Ну это вообще легко. Если число положительное, то умножение — это просто удлинение вектора. Направление при этом сохраняется. Пример можете видеть на рисунке.
Умножить на (−1)(-1)(−1) — это просто изменить направления вектора на противоположное.
Умножить на другое отрицательное число — это просто изменить направление на противоположное и удлинить вектор в соответствующее число раз.
Дан вектор f⃗vec{f}f⃗.
Запишите подряд, без пробелов, номера векторов 0,5f⃗0,5vec{f}0,5f⃗ и −2f⃗-2vec{f}−2f⃗.
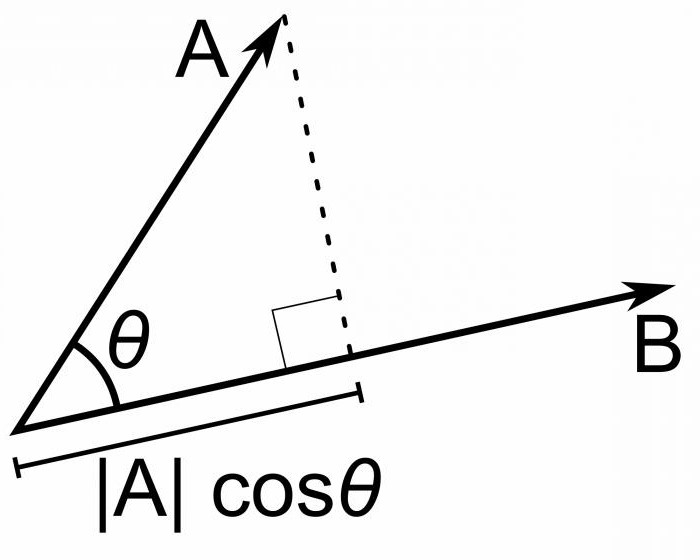
Самое частое, что делают с векторами, — это нахождение их проекций. Об этом читайте в следующей статье — “Проектирование векторов на оси”.
Источник