При какой минимальной температуре между рельсами исчезнет зазор
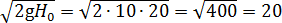
При температуре 0 °C рельс имеет длину L0 = 10м. При прокладке путей между рельсами оставилизазор в 4,5 мм.
При возрастании температуры будет происходить тепловое расширение рельса, и его длина будет меняться по закону L(t°) = L0 (1 +αt°), где α = 1,2·10-5 (°C)-1 — коэффициент теплового расширения, t° — температура (в градусах Цельсия). При какой минимальной температуре между рельсами исчезнет зазор? (Ответ выразите в градусах Цельсия.)
Решение.
Зазор – это то расстояние, которое оставляют между рельсами, для того, чтобы они могли расширяться при нагревании. А нагревание происходит вследствие трения, возникающего при прохождении поезда по рельсам.
Выразим зазор в метрах: 4,5 мм = 4,5 · 10-3 м.
L(t°) = L0 + зазор – длина рельса при удлинении после нагревания на t°.
С другой стороны L(t°) = L0(1+α·t°). Приравняем правые части равенств, подставим данные величины, раскроем скобки, получим:
10 + 4,5·10-3 = 10 + 10·1,2·10-5 ·t° –> t°·12·10-5 = 4,5·10-3 –> t°=450 / 12 = 37,5°.
Ответ: 37,5
При температуре 0 °C рельс имеет длину L0 = 12,5м. При прокладке путей между рельсами оставили зазор в 6 мм.
При возрастании температуры будет происходить тепловое расширение рельса, и его длина будет меняться по закону L(t°) = L0 (1 +αt°), где α = 1,2·10-5 (°C)-1 — коэффициент теплового расширения, t° — температура (в градусах Цельсия). При какой минимальной температуре между рельсами исчезнет зазор? (Ответ выразите в градусах Цельсия.)
Ответ: 40.
При температуре 0 °C рельс имеет длину L0 = 15м. При прокладке путей между рельсами оставилизазор в 6,3 мм.
При возрастании температуры будет происходить тепловое расширение рельса, и его длина будет меняться по закону L(t°) = L0 (1 +αt°), где α = 1,2·10-5 (°C)-1 — коэффициент теплового расширения, t° — температура (в градусах Цельсия). При какой минимальной температуре между рельсами исчезнет зазор? (Ответ выразите в градусах Цельсия.)
Ответ: 35.
После дождя уровень воды в колодце может повыситься. Мальчик определяет его, измеряя время падения t небольших камушков в колодец и рассчитывая по формуле h = -5t2. До дождя время падения камушков составляло 0,6 с. На какую минимальную высоту должен подняться уровень воды после дождя, чтобы измеряемое время изменилось больше, чем на 0,2 с? (Ответ выразите в м.)
Ответ: 1.
После дождя уровень воды в колодце может повыситься. Мальчик определяет его, измеряя время падения t небольших камушков в колодец и рассчитывая по формуле h = -5t2. До дождя время падения камушков составляло 1 с. На какую минимальную высоту должен подняться уровень воды после дождя, чтобы измеряемое время изменилось больше, чем на 0,2 с? (Ответ выразите в м.)
Ответ: 1,8.
После дождя уровень воды в колодце может повыситься. Мальчик определяет его, измеряя время падения t небольших камушков в колодец и рассчитывая по формуле h = -5t2. До дождя время падения камушков составляло 0,8 с. На какую минимальную высоту должен подняться уровень воды после дождя, чтобы измеряемое время изменилось больше, чем на 0,1 с? (Ответ выразите в м.)
Ответ: 0,75.
Пусть h1 – уровень воды до дождя, h2 – уровень воды после дождя, t1 – время падения камешка до поверхности до дождя, t2 – время падения после дождя.
За нулевую отметку принимаем точку, лежащую на поверхности земли, тогда h1 и h2 – координаты уровней воды и они отрицательны, что можно видеть из формулы h = – 5t2.
После дождя уровень воды повысился на |h1 – h2| метра.
По условию t1=0,6c, а t2 уменьшилось более, чем на 0,2 с, т.е. t2 ≤ 0,4 c.
|h1 – h2| = | -5·t12 – (-5·t22)| = | -5·0,62 +5·0,42| = 5|0,62 – 0,42| = 5·0,2 = 1(метр).
h = – 5t2.
h1=h(0,6) = -5*0,36= -1,8
h2=h(0,4) = -5*0,16 = -0,8
h2-h1 = -0,8-(-1,8) = 1
Т.е. после дождя прежний уровень повысится на 1 метр.
При температуре 0° С рельс имеет длину l0 = 20 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону l(t°) = l0(1 + a·t°), где a = 1,2·10-5(°C)-1 — коэффициент теплового расширения, t° — температура (в градусах Цельсия).
Удлинение рельса – это и есть зазор, только 3мм надо выразить в метрах.
l(t°) – l0 =0,003 –> 20(1 + 1,2·10-5 ·t°) – 20 = 0,003 –> 24·10-5 ·t° = 3·10-3 –> t°= 12.5°C
Источник
5 января 2012
Часто бывает, что в одной задаче B12 присутствует и функция, и формула. В таких задачах кроме основной переменной присутствуют дополнительные неизвестные, значения которых надо искать где-то в тексте.
Общая схема решения почти ничем не отличается от задач с формулами (см. урок «Работа с формулами в задаче B12»). В двух словах: найти в тексте числа и подставить их в исходную формулу. Если все сделать правильно, получится стандартное уравнение с одной переменной.
Задача. В ходе распада радиоактивного изотопа его масса уменьшается по закону:
где m0 (мг) — начальная масса изотопа, t (мин) — время, прошедшее от начального момента, T (мин) — период полураспада. В начальный момент времени масса изотопа m0 = 56 мг. Период его полураспада T = 7 мин. Через сколько минут масса изотопа будет равна 7 мг?
По условию, известны следующие величины: m0 = 56; T = 7. Подставим их в функцию — получим m(t) = 56 · 2−t/7. Требуется найти момент, когда m(t) = 7 мг. Составим и решим уравнение:
56 · 2−t/7 = 7;
2−t/7 = 1/8 — разделили все на 56;
2−t/7 = 2−3 — представили 1/8 как 2−3;
−t/7 = −3;
t = 21.
Задача. Для одного из предприятий-монополистов зависимость объема спроса на продукцию q (единиц в месяц) от ее цены p (тыс. руб.) задается формулой: q = 75 − 5p. Определите максимальный уровень p цены (в тыс. руб.), при котором значение выручки предприятия за месяц r = q · p составит не менее 270 тыс. руб.
Итак, у нас есть функция r = q · p, причем q — неизвестная величина. Более того, переменная q сама является функцией: по условию, q = 75 − 5p. Подставим это выражение в функцию r. Получим:
r = (75 − 5p) · p = 75p − 5p2.
Теперь у нас есть функция, выражающая прибыль через цену. Все цены установлены в тысячах рублей — это следует из условия. Также, по условию, прибыль должна быть не менее 270 тыс. руб., поэтому можно написать r = 270. Составим и решим уравнение:
270 = 75p − 5p2;
5p2 − 75p + 270 = 0 — перенесли все влево;
p2 − 15p + 54 = 0 — разделили все на 5;
… (решаем квадратное уравнение)
p1 = 6; p2 = 9.
Поскольку нас интересует наибольшая цена, выбираем p2 = 9.
Задача. При температуре 0 °С рельс имеет длину l0 = 20 метров. При прокладке путей между рельсами оставили зазор в 9 мм. При возрастании температуры будет происходить тепловое расширение рельса, и его длина будет меняться по закону l(t) = l0 · (1 + a · t), где a = 1,2 · 10−5 (°C)−1 — коэффициент теплового расширения, t — температура (в градусах Цельсия). При какой минимальной температуре зазор между рельсами исчезнет? Ответ выразите в градусах Цельсия.
Изначально нам известны две величины: l0 = 20 и a = 1,2 · 10−5. Самый тонкий момент — понять, чему равно l(t). А именно: зазор исчезнет, когда рельс удлинится на эти самые 9 мм. Была длина 20 метров, а стала — 20 метров + 9 мм.
Переведем все в метрическую систему. В одном метре 1000 мм, поэтому 9 мм = 9 · 10−3 м. Итого, l(t) = 20 + 9 · 10−3. Оставим эту запись именно в таком виде, не будем складывать. Получилось уравнение:
20 + 9 · 10−3 = 20 · (1 + 1,2 · 10−5 · t).
Раскроем скобки — и после очевидных преобразований уравнение станет совсем простым:
20 + 9 · 10−3 = 20 + 20 · 1,2 · 10−5 · t;
9 · 10−3 = 24 · 10−5 · t — убрали с обеих сторон число 20.
Умножим обе стороны на 105 и получим:
9 · 10−3 + 5 = 24 · 10−5 + 5 · t;
9 · 102 = 24t — обычное линейное уравнение;
t = 900/24 = 37,5.
Как видите, задача про рельсы оказалась довольно сложной. И многие, кто писал пробный ЕГЭ по математике, с этой задачей не справились. В большинстве случаев ученики забывали, что итоговая длина l(t) — это сумма исходной длины l0 и удлинения, которое еще надо перевести в метры.
Общие выводы из приведенных решений:
- Иногда в задачах о радиоактивных изотопах указывают название вещества — не обращайте внимания на это. Хоть медь-64, хоть ксенон-133 — что угодно. Эти числа не участвуют в решении, а только засоряют текст задачи. Возможно, составители задач делают это намеренно;
- В задачах о предприятиях-монополистах не стоит пугаться единиц измерений. Даже если это сотни тысяч рублей, не надо приписывать нули к указанным в задаче числам. Используйте то, что дано — и получите правильный ответ;
- Когда речь идет о рельсах, важно понимать, что l(t) — это длина всего рельса, а не только его удлинение. Само удлинение (или зазор) надо перевести в метры. Например, 4,5 мм — это 4,5 · 10−3 м. Кроме того, не спешите складывать длину рельса и зазор. Лучше раскройте скобки — формула сложная, но объем вычислений сократится многократно. И не надо вычислять 10−5, а то получится одна стотысячная и будет очень грустно.
Сложные задачи B12
Но рельсы — это еще не все! Существуют еще более сложные задачи, требующие действительно грамотных размышлений. По сравнению с ними даже рельсы отдыхают. Вероятность нарваться на подобную задачу в настоящем ЕГЭ невелика, но знать, как они решаются, совершенно необходимо.
Рассмотрим две такие задачи. Они действительно предлагались на пробном ЕГЭ по математике. Справились с ними лишь единицы.
Задача. Для определения эффективной температуры звезд используют закон Стефана — Больцмана, согласно которому мощность излучения нагретого тела прямо пропорциональна площади его поверхности и четвертой степени температуры:
где σ = 5,7 · 10−8 — постоянная, площадь измеряется в квадратных метрах, температура — в градусах Кельвина, а мощность — в ваттах.
Известно, что некоторая звезда имеет площадь S = (1/128) · 1020 м2, а излучаемая ею мощность P не менее 1,14 · 1025 Вт. Определите наименьшую возможную температуру этой звезды. Ответ дайте в градусах Кельвина.
Конечно, формула с четвертой степенью и числа, содержащие степени десятки, выглядят угрожающе. Но в действительности все не так плохо. Нам известна мощность P, площадь S и постоянная σ. Подставим их в формулу — получим:
1,14 · 1025 = 5,7 · 10−8 · (1/128) · 1020 · T 4.
Единицы измерения не пишем — они только засоряют уравнение. Чтобы упростить решение, умножим обе стороны на 128, а затем по возможности сократим количество множителей. Имеем:
1,14 · 1025 · 128 = 5,7 · 10−8 · (1/128) · 1020 · T 4 · 128;
1,14 · 128 · 1025 = 5,7 · 10−8 · 1020 · T 4 — сократили множители, отмеченные красным;
1,14 · 128 · 1025 = 5,7 · 1012 · T 4;
1,14 · 128 · 1025 − 12 = 5,7 · 1012 − 12 · T 4 — разделили все на 1012;
1,14 · 128 · 1013 = 5,7 · T 4;
1,14 · 128 · 1013 : 5,7 = 5,7 · T 4 : 5,7 — делим все на 5,7;
0,2 · 128 · 1013 = T 4 — потому что 1,14 : 5,7 = 0,2;
2 · 10−1 · 128 · 1013 = T 4 — записали 0,2 = 2 · 10−1;
256 · 1012 = T 4 — группируем двойки и десятки;
T 4 = 1012 · 28 — поскольку 256 = 28;
T = 103 · 22 = 1000 · 4 = 4000.
На последнем шаге мы находим корень 4-й степени. Напомню: извлечение корня понижает степени у каждого множителя.
Вообще говоря, действительных корней в уравнении будет два: T1 = 4000 и T2 = −4000. Но температура в Кельвинах не может быть отрицательной, поэтому второй вариант нас не интересует.
Задача. В боковой стенке высокого цилиндрического бака у самого дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону:
где t — время в секундах, прошедшее с момента открытия крана, H0 = 20 м — начальная высота столба воды, k = 1/50 — отношение площадей поперечных сечений крана и бака, а g — ускорение свободного падения (считайте g = 10 м/с2).
Через сколько секунд после открытия крана в баке останется четверть первоначального объема воды?
Для начала выясним, чему равно искомое H(t). По условию, в баке должна остаться четверть первоначального объема воды. Поэтому H(t) = (1/4) · 20 = 5 м.
Теперь, когда все параметры известны, подставим числа в функцию. Чтобы не усложнять выкладки, заметим следующее:
Таким образом, вместо корня можно смело писать число 20. Имеем:
5 = 20 − 20 · (1/50) · t + (10/2) · (1/50)2 · t2;
0 = 15 − 20 · (1/50) · t + 5 · (1/50)2 · t2 — перенесли все в одну сторону;
(1/50)2 · t2 − 4 · (1/50) · t + 3 = 0 — разделили все на 5.
Сделаем замену переменной: (1/50) · t = x. Тогда (1/50)2 · t2 = x2, и все уравнение перепишется следующим образом:
x2 − 4x + 3 = 0;
(x − 3) · (x − 1) = 0 — корни квадратного уравнения легко угадываются без всякого дискриминанта (см. урок «Теорема Виета»);
x1 = 3; x2 = 1.
Теперь вспоминаем, что такое x. Поскольку мы выполняли замену x = (1/50) · t, имеем:
t = 50x;
t1 = 50 · 3 = 150;
t2 = 50 · 1 = 50.
Итак, у нас два кандидата на ответ: числа 50 и 150. Заметим, что в момент времени t = 100 высота столба воды равна:
H(100) = 20 − 20 · (1/50) · 100 + 5 · (1/50)2 · 1002 = 20 − 40 + 20 = 0.
Другими словами, через t = 100 секунд вода полностью вытечет из бака, и уравнение H(t) теряет физический смысл. Поэтому вариант t = 150 нас не интересует. Остается только t = 50.
В заключение хочу еще раз заострить внимание на последней задаче. Мы отсеяли корень t = 150, поскольку он расположен слишком далеко от старта — там, где исходная формула теряет всякий физический смысл. Сравните:
- С точки зрения математики, перед нами стандартная квадратичная функция, график которой — парабола. И вполне нормально, что квадратное уравнение имеет два корня;
- Но с точки зрения физики, после отметки t = 100 графика вообще не существует. Потому что через 100 секунд вода полностью вытекает из бака, и функция H(t) перестает описывать рассматриваемый процесс. Все, что расположено дальше этой отметки — бред, который нас не интересует.
В задаче про звезды мы выбрали положительный корень, также руководствуясь физическим смыслом. Данные примеры наглядно демонстрируют, насколько опасно «увлекаться» математическими уравнениями без оглядки на реальные условия задач. Будьте внимательны!
Смотрите также:
- Текстовые задачи про рельсы
- Сводный тест по задачам B12 (1 вариант)
- Что такое логарифм
- Следствия из теоремы Виета
- Пробный ЕГЭ по математике 2015: 6 вариант
- Проценты в задачах на наибольшее-наименьшее значение: используем формулы процентов
Источник
На канале было опубликовано несколько постов про 800 метровые рельсовые плети, которые укладывают сегодня в путь.
Публикации собрали достаточно много комментариев и просмотров, что показало актуальность темы.
Материалы по теме:
Производство 800 метровых рельс.
Перевозка 800 метровых рельс.
Выгрузка 800 метровых рельс.
Также читателей заинтересовал вопрос – “каким образом происходит компенсация температурных изменений в таких длинных рельсовых плетях?“.
Так как при нагревании тела расширяются, то при нагревании рельсовой плети происходит ее равномерное удлинение. Учитывая этот факт, при эксплуатации “бархатного” пути, необходимо предусматривать меры, позволяющие компенсировать эти температурные изменения.
Существует два варианта:
1. Укладка звеньевого пути между плетями, так называемых “уравнительных пролетов“.
Данный вариант чаще всего применяется на участках оборудованных автоблокировкой, на которой необходимо применение изолирующих стыков. А также на участках с профилем пути имеющем много кривых малого радиуса.
Уравнительный пролет у сигнальной точки автоблокировки
В данном случает температурные изменения компенсируются стыковыми зазорами между короткими рельсами уравнительных пролетов.
2. Укладка уравнительных приборов между плетями или на станциях, ограничивающий перегон.
Данный вариант применяется в основном на участках скоростного движения, где изолирующие стыки на перегонах не нужны, либо они применяются заводские (клееболтовые), которые вварены в плеть.
Уравнительный прибор отделяющий перегонную плеть от первой станционной стрелки
Плеть может достигать длины в перегон. А на входе на станцию оборудуются уравнительные приборы, которые компенсируют температурные изменения заходящих на станцию плетей.
Для нормальной работы бесстыкового пути существует такой критерий как “температура закрепления” рельсовой плети. Данный показатель один их самых главных для такого типа пути. Для каждого участка железных дорог РЖД он разный и устанавливается он в зависимости от местных климатических условий.
Если температура наружного воздуха в момент укладки плети ниже, чем требуемая температура закрепления, то для ввода в оптимальный температурный интервал плети натягивают с помощью гидравлических натяжителей.
Натяжители подтягивают рельс до соединения с соседним рельсом. После чего рельсы соединяются стыковыми накладками и плеть фиксируется шпальными креплениями.
Для трамвайных путей, где требования не такие жесткие как на железных дорогах, где меньшие скорости движения и нагрузки на путь, где нет таких длинных плетей, для компенсации температурных колебаний укладываются уравнительные стыки.
Уравнительный стык на трамвайной линии в Н.Новгороде
Трамвайный уравнительный стык имеет более простую конструкцию и менее прихотлив в эксплуатации и обслуживании.
Понравилась публикация ставьте палец вверх и подписывайтесь на канал! Читайте другие материалы на канале.
Читайте также:
Северный широтный ход – второе рождение.
Как едет машинист не видя светофоров?
Первый рельсовый автобус РА-3 вышел из ворот завода.
32-осные вагоны гиганты, для чего они?
Как пропустить больше электричек? Поможет автоблокировка!
Источник