При какой температуре средняя арифметическая
Средняя арифметическая разность температур. (Arithmetic Mean Temperature Difference – AMTD), Средняя логарифмическая разность температур (Logarithmic Mean Temperature Difference – LMTD или DTLM).
Средняя арифметическая разность температур и средняя логарифмическая разность температур используется для оценки теплообмена, при процессе конвекционной теплопередачи.
В связи с законом Ньютона-Римана, процесс теплопередачи зависит от мгновенной разницы температур холодного и теплого вещества.
- в процессе теплопередачи разница температур меняется по мере прохождения жидкости через теплообменник и в зависимости от времени нахождения (скорость потока).
Средняя разность температур.
Средняя разность температур в процессе передачи тепла зависит от направления потока жидкости, включенного в процесс. Главная и второстепенная жидкости в процессе теплопередачи могут
протекать в одном направлении – параллельный поток или сонаправленные потоки
в разных направлениях – противоположнонаправленные потоки
или перпендикулярные друг другу – перекрестный поток.
Если в первичном контуре рабочее тело – насыщенный пар, то первичная температура может считаться постоянной, т.к процесс теплопередачи идет как результат изменения агрегатного состояния. Температурная кривая первичного потока не зависит от направления потока.
Средняя логарифмическая разность температур (Logarithmic Mean Temperature Difference – LMTD или DTLM).
Изменение температуры рабочей среды во вторичном контуре – нелинейно. Именно поэтому её лучше представить в логарифмическом виде:
LMTD = (dto – dti) / ln(dto / dti) (1)
где
LMTD = Средняя логарифмическая разность температур (oF, oC)
dti = tpi – tsi = разница входящих температур первичного и вторичного контура. (inlet primary и secondary) (oF, oC)
dto = tpo – tso = разница выходящих температур первичного и вторичного контура. (outlet primary и secondary) (oF, oC)
Средняя логарифмическая разность температур всегда меньше средней арифметической разности температур.
Средняя арифметическая разность температур. (Arithmetic Mean Temperature Difference – AMTD)
Более простой, но менее точный способ вычислить разницу температур.
AMTD выражается как:
AMTD = (tpi + tpo) / 2 – (tsi + tso) / 2 (2)
где
AMTD = Средняя арифметическая разность температур (oF, oC)
tpi = входная температура первичного контура (inlet primary) (oF, oC)
tpo = выходная температура первичного контура (outlet primary) (oF, oC)
tsi = входная температура вторичного контура (inlet secondary) (oF, oC)
tso = выходная температура вторичного контура (outlet secondary) (oF, oC)
Средняя арифметическая разность температур даст удовлетворительное приближения для средней разности температур, когда наименьшая из разниц входящей и выходищей температур будет больше чем половина наибольшей разницы входящей и выходящей температур.
Когда тепло передается как результат изменения фазового состояния (конденсация или испарение), температура первичного и вторичного контура остается постоянной.
tp1 = tp2
или
ts1 = ts2
Калькулятор средних арифметических и логарифмических разниц температур
Калькулятор ниже используется для вычисления средних арифметических и логарифмических разниц температур в противоположных и параллельных потоках.
Пример – Средняя арифметическая и логарифмическая разница температур, Горячая вода нагревает воздух
Горячая вода температурой 80 oC нагревает воздух с 0 oC до 20 oC в параллельном потоке теплообмена. Вода покидает теплообменник при температуре 60 oC.
Средняя арифметическая разница температур вычисляется:
AMTD = ((80 oC) + (60 oC)) / 2 – ((0 oC) + (20 oC)) / 2
= 60 oC
Средняя логарифмическая разница температур вычисляется:
LMTD = ((60 oC) – (20 oC)) – ((80 oC) – (0 oC))) / ln(((60 oC) – (20 oC)) / ((80 oC) – (0 oC)))
= 57.7 oC
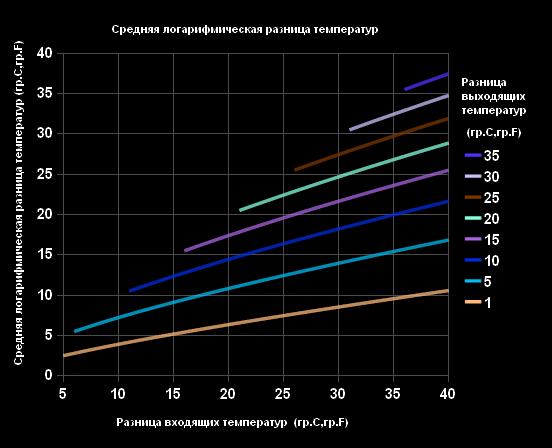
График логарифмической разницы температур
Источник
При какой температуре Т средняя арифметическая скорость атомов гелия станет
равной второй космической скорости v2 @ 11,2 км/с?
Решение
1. Запишем
уравнение для средней квадратичной скорости атомов гелия и выразим из него температуру
. (1)
2. Подставим в уравнение (1) вместо средней
арифметической скорости значение второй космической скорости
. (2)
1.3.13. При какой температуре Т молекулы
кислорода имеют такую же среднюю квадратичную скорость <vкв> как и молекулы водорода при температуре
Т1 = 100 К ?
Решение
1. Запишем уравнения средних квадратичных
скоростей для заданных газов
. (1)
2. Приравняем уравнения для средних арифметических
скоростей
, (2)
и выразим искомую температуру
Т
. (3)
1.3.14. Колба вместимостью V = 4×103 м3содержит некоторый газ массой
m = 6×10 4 кг под давлением р =
200 кПа. Определить среднюю квадратичную скорость <vкв> молекул газа.
Решение
1. Запишем уравнение Клапейрона Менделеева
, (1)
и перепишем следующим образом
. (2)
2. Воспользуемся далее
уравнением для <vкв>
, (3)
и подставим в него значение
комплекса RT/m из уравнения (2)
. (4)
1.3.15. Определить среднюю квадратичную скорость
и среднюю кинетическую энергию молекул гелия и аргона, находящихся в одном сосуде
с температурой Т = 1200 К.
Решение
1. Скорость молекул, находящихся
при одинаковой температуре, судя по уравнению (3) предыдущей задачи, определяется
их молярной массой, mHe = 4×10 3кг/моль, mAr
= 40 10 3 кг/моль
, (1)
. (2)
2. Молекулы заданных газов одноатомные, поэтому
они обладают только тремя поступательными степенями свободы i = 3, их суммарная
энергия определится уравнением
. (3)
3. Как следует из уравнения
(3), кинетическая энергия поступательного движения молекул при одинаковом числе
степеней свободы зависит только от температуры. Другими словами
. (4)
1.3.16. Взвешенные в воздухе твёрдые частички
совершают подобно молекулам, хаотическое тепловое движение при температуре Т =
300 К. Масса одной частички составляет m = 10 10 г. Определить среднее значение
квадратичной скорости частичек.
Решение
1. Поскольку взвешенные
в воздухе частички движутся хаотично и силой тяжести можно пренебречь, то их квадратичную
скорость можно определить, воспользовавшись уравнением
.
1.3.17. Во сколько раз среднеквадратичная скорость молекул кислорода О2 отличается
от скорости пылинки массой m = 10 11 кг, находящейся среди молекул кислорода?
Решение
1. Пылинка и молекулы кислорода находятся при одинаковой температуре,
поэтому отношение их средних скоростей можно записать следующим образом
.
1.3.18. Определить среднюю арифметическую скорость
молекул некоторого газа <vар>, если их среднеквадратичная скорость равна
<vкв> = 1000 м/с.
Решение
1. Найдём отношение среднеквадратичной
и средней арифметической скорости для одной и той же молекулы, находящейся при
температуре Т
. (1)
2. Из уравнения (1) следует, что
средняя арифметическая скорость молекулы определится как, <vар> = <vкв>/1,085
@ 922 м/с.
1.3.19. Определить
наиболее вероятную скорость молекул водорода vв при температуре Т = 400 К.
Решение
1. Воспользуемся уравнением вероятной скорости
.
1.3.20. Какой импульс при ударе о стенку сообщает
молекула ксенона, разогретая в баллоне осветительной лампы до температуры 1 кК?
Скорость молекулы принять равной среднеквадратичной скорости.
Решение
1. Для определения импульса молекулы при её рассмотрении как твёрдой частицы необходимо
установить массу. Это можно сделать, исходя из того, что молярная масса представляет
собой произведение массы одной молекулы на количество молекул в одном моле, т.е.
. (1)
2. Среднеквадратичная скорость молекулы,
как известно, определяется как
, (2)
импульс молекулы в этом
случае запишется следующим образом
. (3)
Перпендикулярно плечу диполя с электрическим моментом р = 12 пКл м возбуждено однородное электрическое поле напряжённостью Е = 300 кВ/м. Под действием поля диполь начинает поворачиваться относительно оси, проходящей через его центр. Определить угловую скорость диполя в момент прохождения им положения равновесия. Момент инерции диполя относительно оси, перпендикулярной плечу и проходящей через центр диполя равен J = 2 10 9 кг м2
Источник
При какой температуре Т средняя арифметическая скорость атомов гелия станет
равной второй космической скорости v2 @ 11,2 км/с?
Решение
1. Запишем
уравнение для средней квадратичной скорости атомов гелия и выразим из него температуру
. (1)
2. Подставим в уравнение (1) вместо средней
арифметической скорости значение второй космической скорости
. (2)
1.3.13. При какой температуре Т молекулы
кислорода имеют такую же среднюю квадратичную скорость <vкв> как и молекулы водорода при температуре
Т1 = 100 К ?
Решение
1. Запишем уравнения средних квадратичных
скоростей для заданных газов
. (1)
2. Приравняем уравнения для средних арифметических
скоростей
, (2)
и выразим искомую температуру
Т
. (3)
1.3.14. Колба вместимостью V = 4×103 м3содержит некоторый газ массой
m = 6×10 4 кг под давлением р =
200 кПа. Определить среднюю квадратичную скорость <vкв> молекул газа.
Решение
1. Запишем уравнение Клапейрона Менделеева
, (1)
и перепишем следующим образом
. (2)
2. Воспользуемся далее
уравнением для <vкв>
, (3)
и подставим в него значение
комплекса RT/m из уравнения (2)
. (4)
1.3.15. Определить среднюю квадратичную скорость
и среднюю кинетическую энергию молекул гелия и аргона, находящихся в одном сосуде
с температурой Т = 1200 К.
Решение
1. Скорость молекул, находящихся
при одинаковой температуре, судя по уравнению (3) предыдущей задачи, определяется
их молярной массой, mHe = 4×10 3кг/моль, mAr
= 40 10 3 кг/моль
, (1)
. (2)
2. Молекулы заданных газов одноатомные, поэтому
они обладают только тремя поступательными степенями свободы i = 3, их суммарная
энергия определится уравнением
. (3)
3. Как следует из уравнения
(3), кинетическая энергия поступательного движения молекул при одинаковом числе
степеней свободы зависит только от температуры. Другими словами
. (4)
1.3.16. Взвешенные в воздухе твёрдые частички
совершают подобно молекулам, хаотическое тепловое движение при температуре Т =
300 К. Масса одной частички составляет m = 10 10 г. Определить среднее значение
квадратичной скорости частичек.
Решение
1. Поскольку взвешенные
в воздухе частички движутся хаотично и силой тяжести можно пренебречь, то их квадратичную
скорость можно определить, воспользовавшись уравнением
.
1.3.17. Во сколько раз среднеквадратичная скорость молекул кислорода О2 отличается
от скорости пылинки массой m = 10 11 кг, находящейся среди молекул кислорода?
Решение
1. Пылинка и молекулы кислорода находятся при одинаковой температуре,
поэтому отношение их средних скоростей можно записать следующим образом
.
1.3.18. Определить среднюю арифметическую скорость
молекул некоторого газа <vар>, если их среднеквадратичная скорость равна
<vкв> = 1000 м/с.
Решение
1. Найдём отношение среднеквадратичной
и средней арифметической скорости для одной и той же молекулы, находящейся при
температуре Т
. (1)
2. Из уравнения (1) следует, что
средняя арифметическая скорость молекулы определится как, <vар> = <vкв>/1,085
@ 922 м/с.
1.3.19. Определить
наиболее вероятную скорость молекул водорода vв при температуре Т = 400 К.
Решение
1. Воспользуемся уравнением вероятной скорости
.
1.3.20. Какой импульс при ударе о стенку сообщает
молекула ксенона, разогретая в баллоне осветительной лампы до температуры 1 кК?
Скорость молекулы принять равной среднеквадратичной скорости.
Решение
1. Для определения импульса молекулы при её рассмотрении как твёрдой частицы необходимо
установить массу. Это можно сделать, исходя из того, что молярная масса представляет
собой произведение массы одной молекулы на количество молекул в одном моле, т.е.
. (1)
2. Среднеквадратичная скорость молекулы,
как известно, определяется как
, (2)
импульс молекулы в этом
случае запишется следующим образом
. (3)
Источник
Средняя арифметическая разность температур. (Arithmetic Mean Temperature Difference – AMTD), Средняя логарифмическая разность температур (Logarithmic Mean Temperature Difference – LMTD или DTLM).
Средняя арифметическая разность температур и средняя логарифмическая разность температур используется для оценки теплообмена, при процессе конвекционной теплопередачи.
В связи с законом Ньютона-Римана, процесс теплопередачи зависит от мгновенной разницы температур холодного и теплого вещества.
- в процессе теплопередачи разница температур меняется по мере прохождения жидкости через теплообменник и в зависимости от времени нахождения (скорость потока).
Средняя разность температур.
Средняя разность температур в процессе передачи тепла зависит от направления потока жидкости, включенного в процесс. Главная и второстепенная жидкости в процессе теплопередачи могут
протекать в одном направлении – параллельный поток или сонаправленные потоки
в разных направлениях – противоположнонаправленные потоки
или перпендикулярные друг другу – перекрестный поток.
Если в первичном контуре рабочее тело – насыщенный пар, то первичная температура может считаться постоянной, т.к процесс теплопередачи идет как результат изменения агрегатного состояния. Температурная кривая первичного потока не зависит от направления потока.
Средняя логарифмическая разность температур (Logarithmic Mean Temperature Difference – LMTD или DTLM).
Изменение температуры рабочей среды во вторичном контуре – нелинейно. Именно поэтому её лучше представить в логарифмическом виде:
LMTD = (dto – dti) / ln(dto / dti) (1)
где
LMTD = Средняя логарифмическая разность температур (oF, oC)
dti = tpi – tsi = разница входящих температур первичного и вторичного контура. (inlet primary и secondary) (oF, oC)
dto = tpo – tso = разница выходящих температур первичного и вторичного контура. (outlet primary и secondary) (oF, oC)
Средняя логарифмическая разность температур всегда меньше средней арифметической разности температур.
Средняя арифметическая разность температур. (Arithmetic Mean Temperature Difference – AMTD)
Более простой, но менее точный способ вычислить разницу температур.
AMTD выражается как:
AMTD = (tpi + tpo) / 2 – (tsi + tso) / 2 (2)
где
AMTD = Средняя арифметическая разность температур (oF, oC)
tpi = входная температура первичного контура (inlet primary) (oF, oC)
tpo = выходная температура первичного контура (outlet primary) (oF, oC)
tsi = входная температура вторичного контура (inlet secondary) (oF, oC)
tso = выходная температура вторичного контура (outlet secondary) (oF, oC)
Средняя арифметическая разность температур даст удовлетворительное приближения для средней разности температур, когда наименьшая из разниц входящей и выходищей температур будет больше чем половина наибольшей разницы входящей и выходящей температур.
Когда тепло передается как результат изменения фазового состояния (конденсация или испарение), температура первичного и вторичного контура остается постоянной.
tp1 = tp2
или
ts1 = ts2
Калькулятор средних арифметических и логарифмических разниц температур
Калькулятор ниже используется для вычисления средних арифметических и логарифмических разниц температур в противоположных и параллельных потоках.
Пример – Средняя арифметическая и логарифмическая разница температур, Горячая вода нагревает воздух
Горячая вода температурой 80 oC нагревает воздух с 0 oC до 20 oC в параллельном потоке теплообмена. Вода покидает теплообменник при температуре 60 oC.
Средняя арифметическая разница температур вычисляется:
AMTD = ((80 oC) + (60 oC)) / 2 – ((0 oC) + (20 oC)) / 2
= 60 oC
Средняя логарифмическая разница температур вычисляется:
LMTD = ((60 oC) – (20 oC)) – ((80 oC) – (0 oC))) / ln(((60 oC) – (20 oC)) / ((80 oC) – (0 oC)))
= 57.7 oC
График логарифмической разницы температур
Источник
| Другие темы раздела | |
| Термодинамика и МКТ При какой температуре средняя квадратичная скорость атомов гелия станет равной 2-ой космической скорости https://www.cyberforum.ru/ mkt-thermodynamics/ thread1493370.html 2)при какой температуре средняя квадратичная скорость атомов гелия станет равной 2-ой космической скорости 11,2км/с? | Найдите период малых колебаний старжня Термодинамика и МКТ 1)однородный стержень дилиной 0.5 м колеблется вокруг горизантальной оси ,перпендикулярной к стержню и проходящей через его верхний конец!найдите период малых колебаний старжня. |
| Вычислить вес столба атмосферы с площадью основания 1 м2 и высотой 1 км Термодинамика и МКТ 2. Вычислить вес столба атмосферы с площадью основания 1 м2 и высотой 1 км, если нижнее основание находится : а) на уровне моря, б) на высоте 2 км над поверхностью Земли. Давление на поверхности… | Термодинамика и МКТ За сколько циклов насос откачает тот же сосуд до давления 380 мм ртст? 1. Насос откачивает сосуд от начального давления 760 мм рт.ст. до давления 0.1 мм рт.ст. за 129 циклов. За сколько циклов этот насос откачает тот же сосуд до давления 380 мм рт.ст.? Ответ: 10. https://www.cyberforum.ru/ mkt-thermodynamics/ thread1493360.html |
| Термодинамика и МКТ Отношение коэффициента теплопроводности кислорода к коэффициенту теплопроводности азота https://www.cyberforum.ru/ mkt-thermodynamics/ thread1493355.html 10. Кислород и азот находятся при одинаковых температурах и давлении. Найти отношение коэффициента теплопроводности кислорода к коэффициенту теплопроводности азота. Диаметр молекул этих газов считать… | Термодинамика и МКТ Найти отношение коэффициента внутреннего трения углекислого газа к коэффициенту внутреннего трения азота 9. Углекислый газ и азот находятся при одинаковых температурах и давлении. Найти отношение коэффициента внутреннего трения углекислого газа к коэффициенту внутреннего трения азота. Диаметр молекул… |
| Найти эффективный диаметр молекулы кислорода Термодинамика и МКТ 8. Найти эффективный диаметр молекулы кислорода, считая известными число Авогадро NА=6,021023 моль-1 и поправку Ван-дер-Вальса b=3,1710-5 м3/моль. Ответ: а) d=2,910-10 м; б)… | Термодинамика и МКТ Пользуясь уравнением Ван-дер-Ваальса, найти, во сколько раз надо увеличить температуру газа 7. В закрытом сосуде объемом 0,5 м3 находится 0,6 киломолей углекислого газа при давлении 30 кПа. Пользуясь уравнением Ван-дер-Ваальса, найти, во сколько раз надо увеличить температуру газа, чтобы… https://www.cyberforum.ru/ mkt-thermodynamics/ thread1493352.html |
| Термодинамика и МКТ Найти КПД цикла тепловой машины, работающей по циклу Карно https://www.cyberforum.ru/ mkt-thermodynamics/ thread1493351.html 6. Тепловая машина, работающая по циклу Карно, совершает за один цикл работу А=2,94 кДж и отдает за один цикл холодильнику количество теплоты Q2=13,4 кДж. Найти КПД цикла. Ответ: а) η=18%; б)… | Термодинамика и МКТ Какое количество теплоты было сообщено газу? 5. При изобарическом расширении двухатомного газа была совершена работа А=156,8 Дж. Какое количество теплоты было сообщено газу? Ответ: а) ΔU=580 Дж; б) ΔU=570 Дж; в) ΔU=560 Дж; г)… https://www.cyberforum.ru/ mkt-thermodynamics/ thread1493350.html |
0 / 0 / 0 Регистрация: 14.06.2010 Сообщений: 5 | |
| |
15.06.2010, 15:42. Просмотров 862. Ответов 0 3)при какой температуре средняя арифметическая скорость молекул азота и кислорода отличаются на 20м/с ? Вернуться к обсуждению: | |
Источник